This blog notes down all key concepts and properties to remember to be able to solve problems related to GMAT linear and quadratic equations. Many GMAT Data Sufficiency & GMAT Problem Solving questions need basic know-how and knowledge of properties so we can infer if sufficient information is available or not.
This section needs to be revised at least once. Before we delve into quadratic equations, we will take a look at the basic linear equations.
Linear Equations
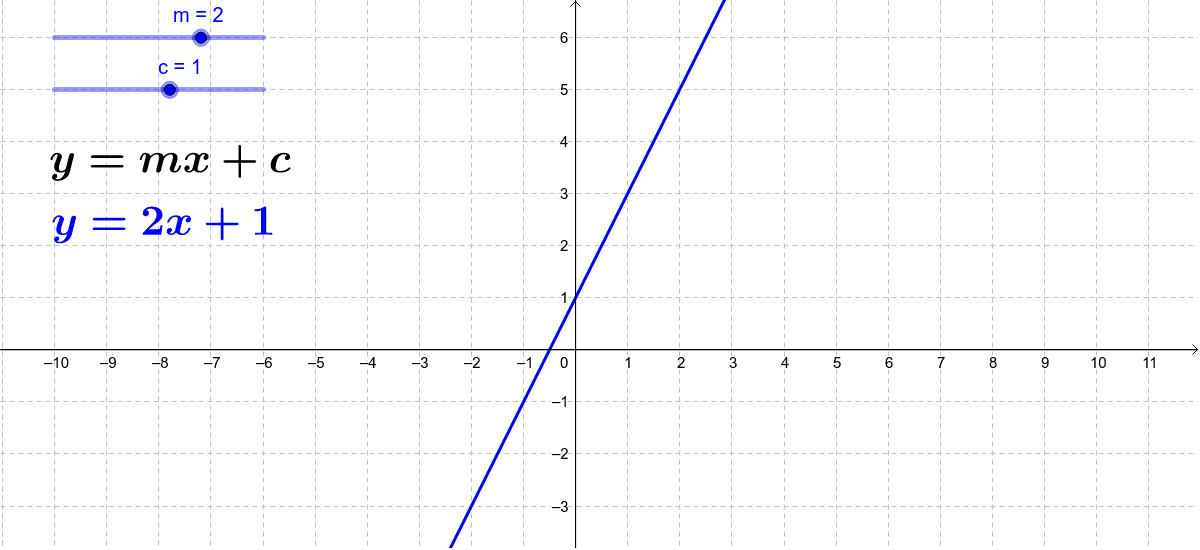
The most basic equation is of the form y = mx + c. Herein, m is the slope and c is the intercept for the equation. We have two variables here to be able to solve for the x and y. We will need at least two equations to solve for two variables.
Though in GMAT, you could solve for y = mx + c if there is additional information available such as the values of x and y being positive integers. This will eliminate any chance of them being 0 as well. Thus, this constraint can help us to be able to get the values of x and y.
Quadratic Equations
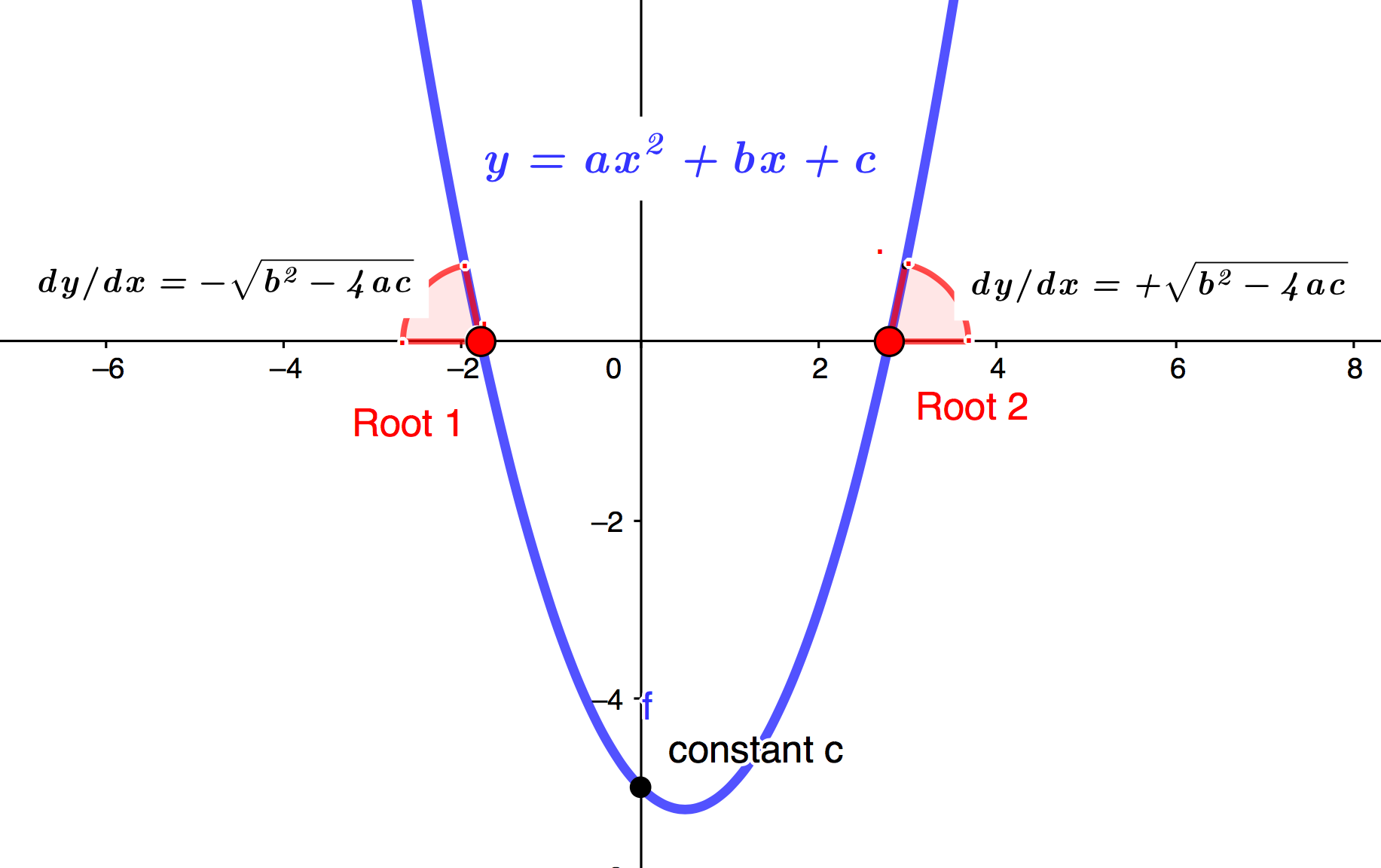
The quadratic equations are equations with degree 2. So, the highest power of the variables is 2. They typically take the form of ax^2 + bx + c = 0. Where a, b, c are constants.
- Roots: The roots for the equations is defined as [-b +/- sqrt(b^2-4ac)]/2a. The image above shows a neat representation of the same.
- Sum/Product: The sum of the roots is (-b/a) and the product of the roots is equivalent to (c/a). Given b and c. We should be able to solve for both the roots. Two equations and two variables.
Plug in Numbers
The key to solving questions with variables within the problem statement is to use numbers to plugin for the variables and use POE aka process of elimination for the equations.
- e.g. Let’s say the problem statement ends up as a probable solution with values of 4K + 4 or 4K – 4.
- We can check for the right answer by pluggin in the value for K and seeing which answers don’t match the actual output.
- The right answers is among the non eliminated options. By plugging in another number, we can further reduce the choices until we end up with one choice.
- This is faster than trying to solve algebraically.