This blog notes down all key properties to remember to be able to infer and use concepts for GMAT permutation and combination related problems. Many GMAT Data Sufficiency problems will need the know-how of the properties so that we can infer if sufficient information is available or not. Thereby knowing these properties will be key, especially for data sufficiency problems.
Combination
Before heading to permutation, the combination is the first thing to understand. Combinations can be defined as a number of ways to select or choose a certain number of items from a sample.
- Here is the formula for combinations which is n choose r.
- Where n is the number of the elements in the sample and r is the number being chosen.
Also when dealing with multiple combinations of events where we have situations of choose C choose A or C choose B. We will add up the count of the combinations. If we are dealing with AND that C chooses A and C to choose B, we will end up multiplying them.
e.g. The number of ways of choosing 4 or 5 balls from a sample of 9 different balls. The answer would be the sum of choosing 4 balls plus the number of ways of choosing 5 balls.
Permutation
Permutations and combinations have to order among the selection as well. This goes beyond just selection and takes the order of the selection into account.
- The permutation formula is a logical addtion to combination.
- The r! is the number of ways of bringing order to the r chosen values thus r!
Filling Up Space
This is basically a subset of Permutations but given the frequency of the problem and the situation, we could go with a separate section. The general problems here are things such as the number of ways of creating a 4 digit number using 6 numbers which are not be repeated. e.g.: From a list of numbers 3,4,7,8,9,5 create a 4 digit number.
- The way to go about it would be _ _ _ _ to fill up the 4 spots where we have 6 choices at the first place. 5 at the second, 4 on the third and so on.
- The final count would thereby come out to be 6*5*4*3 = 360
- This is the filling the space way. The answer for repetition would be 6*6*6*6 = 1296
The problems similar to this often come with certain constraints such as the sample being 0,3,7,8,9,5.
- The first constraint is that we can’t 0 as the first number in the 4 spots since, it won’t be 4 digit number in that case.
- The answer thereby comes out to be 5*5*4*3 = 300
- If we are looking for 4 digit numbers which are even, we have further restrictions.
- In this case, fill up the constaints first than the numbers next.
- The answer would 5*_ _ *1 since only even number is 8. 5*5*4 = 100 combinations is the answer.
GMAT Probability
These questions just require us to calculate the counts like permutations and combinations. The difference being the probability will be the ratio of the number of favourable cases/ total number of cases.
- The numerator is the count of the favourable cases.
- The denominator is the count of the overall sample and the ratio is the probability of obtaining the favourable cases.
Sets
Sets are a unique collection of objects as per set theory with no order among them. In this context, we are mostly dealing with Venn diagrams and the concepts of intersection and union between 2 and 3 sets as a whole.
- The intersection between 2 sets is defined as elements common between A and B.
- The union between 2 sets is defined as the unqiue elements in either of the sets A and B.
- For 3 sets, the different components is given as below.
- We have 3 pairs where we have elements belonging to 2 sets and one combination belonging to all 3 sets.
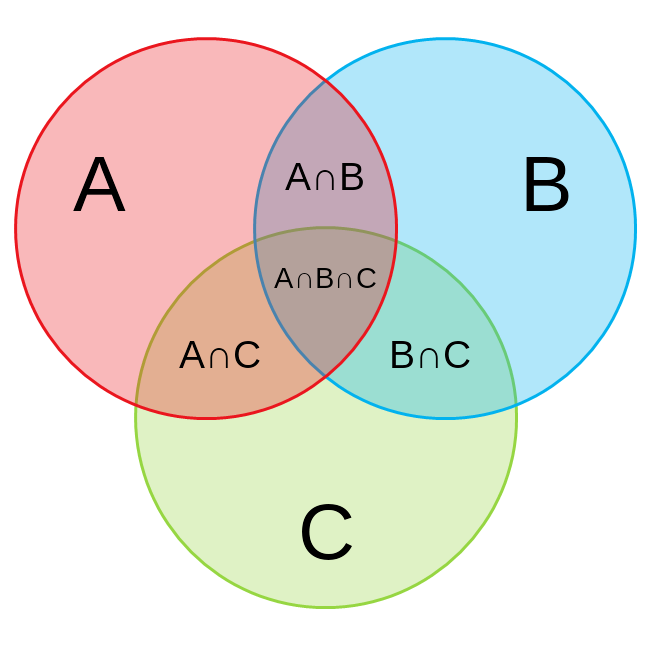
- The formula for union of the 3 sets is mentioned.
- Another way to approach the problem is to write down each exclusive part of the union of set as a variable and represent all combinations in their form.
Pointers
Figure out if the problem statement is a combinatorial or permutations one. The next step is to use the appropriate tool in terms of the formula from either of the two or use the filling the space approach for high constraint problems.
- The number of ways of arranging n elements in a circle is (n-1)!
- This is because, while order is existent in circle, being a circle, there is no starting point to it.




