This blog notes down all key concepts to remember to be able to infer and use for GMAT triangles related problems using formulas. Many GMAT Data Sufficiency problems will need the know-how of the properties so we can infer if sufficient information is available or not. Knowing these properties is key to being at the top of the exam.
Lines Properties
The lines have a few simple properties
- The sum of lines on a straight line is 180 degrees.
- When two straight lines intersect each other, the opposite angles are of the same value
- If sum of two angles is 180 degree, then they are supplementary angles.
- If sum of angles is 90 degrees, they are complementary angles.
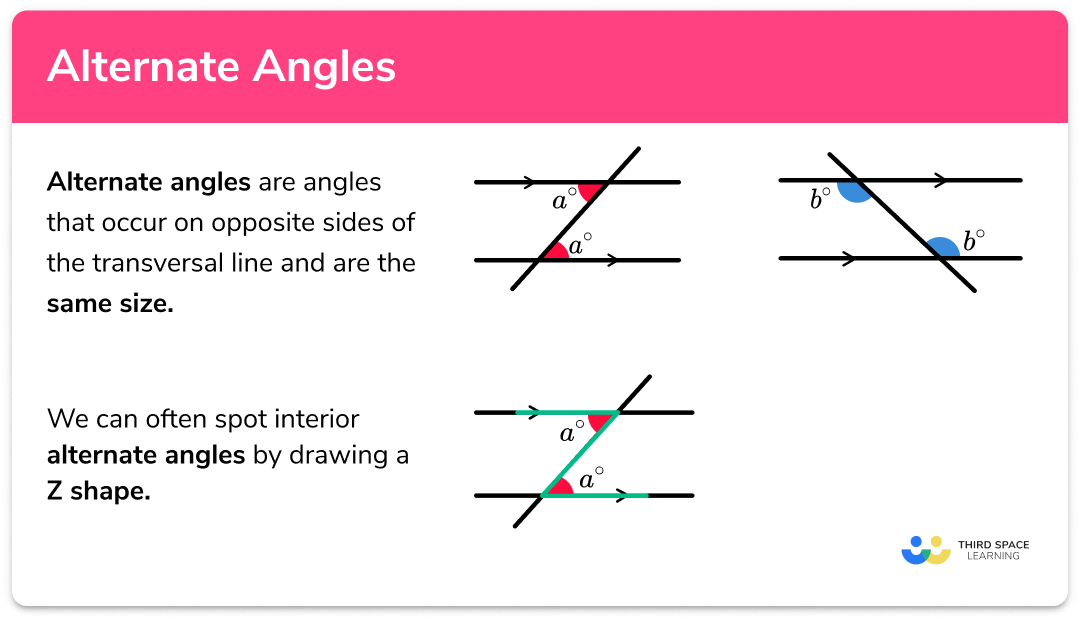
- One more non intuitive but true property is the concept of alternate angles when you have two parallel lines and an intersecting line with the 2.
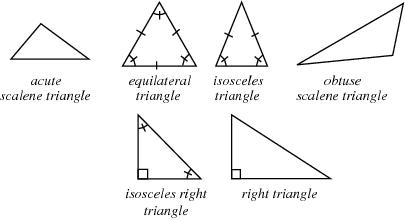
GMAT Triangles Types
Angle Properties
- Internal Angles: The sum of the 3 internal angles is always equal to 180 degrees. This will be irrespective of the type of triangle.
- External Angles: The sum of the 3 external angles is always equal to 360 degrees. An external angle is defined as 180 – internal angle. This property goes further where the external angle is equal to the sum of the two angles other than the corresponding internal angle.
- Sides Property: The sum of two sides is always greater than the third side. This is true for all 3 combinations out of the 3 sides of a triangle. Also, the positive difference between sides is always less than the third side. This is a derivative from the first property.
- Perimeter: Perimeter of a triangle is the sum of the 3 sides of a triangle. Thereby, the sum is always greater than 2 times any side.
- Area: The area of a triangle is defined as (1/2)*(perpendicular)*(base side length). This perpendicular and the base sides can be any of the pair from the 3 sides.
- Another formula to get the area is to use the Hero’s formula which is sqrt(s*(s-a)*(s-b)*(s-c)). Here s stands for the semi perimeter defined as (a + b + c)/2 where a,b,c are the 3 sides of the triangle.

- Pythagoras Theorem: For right-angle triangle. The square of the largest side is equal to the sum of the other two sides.
GMAT Triangles Formulas
- Triangles Types: There are three types of triangles. All sides are different, two are the same and all three are the same.
- This results in interesting case such as all angles in the equilateral triangle being the same.
- Don’t assume which two sides are the same until mentioned in the question when dealing with isosceles triangle.
- The area of an equilateral triangle is given as (sqrt(3)/4)*(a^2) where a is the one of the sides of the triangle.
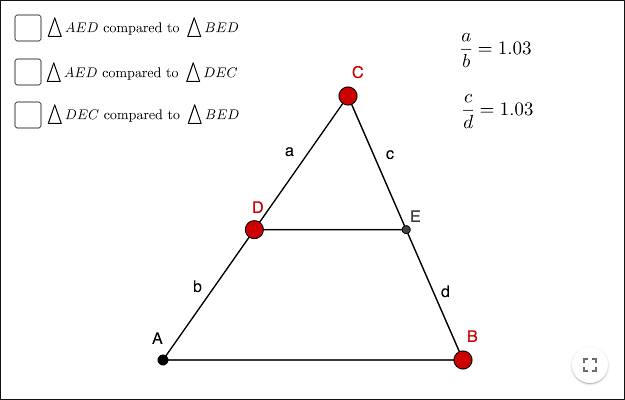
- Similar Triangles: If two triangles have similar angles, the ratio of sides is the same for both of the triangles. Which means (a+b)/(a) = (c+d)/(c)
- This property further aids in the ratio of area. The area of the larger triangle upon smaller is ((c+d)/c)^2.
- The similarity can be inferred if either the angles are similar or if the proportion of the sides is same for the all 3 combinations.