GMAT Quadrilaterals and Polygons

This blog notes down all key concepts and properties to remember to be able to infer and use for GMAT quadrilaterals and polygons related problems. Many GMAT Data Sufficiency problems will need the know-how of the properties so that we can infer if sufficient information is available or not. Thereby knowing these properties will be key, especially for data sufficiency problems.

All Topics Indexed

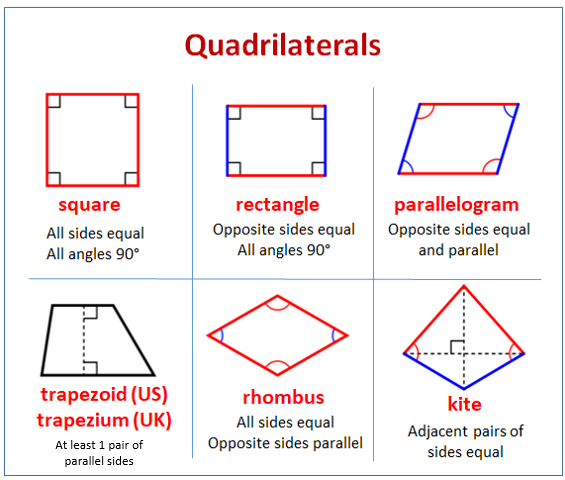
GMAT Quadrilateral Properties

• Internal Angles: The sum of the four internal angles of a quadrilateral is 360 degrees. Similar to the 180 degrees property of triangles.
• Parallelogram: It is a quadrilateral where each of the two sides is parallel to each other. Since the two sides are parallel to each other, the sum of angles on one side is 180 degrees. This would be
  • < A + < B = 180 degrees
  • < C + < D = 180 degrees
  • The opposite angles are the same as well.
  • The opposite sides are of the same length.
  • The parallel sides are equal but the adjacent ones are not necessarily!

• Rectangles: A special case of parallelogram where each of the internal angles is 90 degrees each. On the other hand, the other special property is that the diagonals don’t necessarily bisect at 90 degrees.

• Squares: All sides are equal, each internal angle is 90 degrees while the diagonals bisect each other at 90 degrees.

• Rhombus: Another special case of the parallelogram wherein the internal angles are not necessarily 90 degrees.
  • The area is defined as the (1/2)*(Product of diagonals)
  • All the sides of a rhombus are equal
  • Diagonals bisect each other at 90 degrees.

• Trapezium: The most interesting of all quadrilaterals. Only one pair of sides are parallel while one of the side’s lengths is smaller than the other parallel one.
  • The area can be derived if we the sum of A & B and the height H. The same formula applies for any parallelogram as well where A = B and thus the formula becomes H*Base.
  • The diagonals don’t bisect at 90 degrees.
  • Opposite angles are not necessarily equal though other properties of parallelogram hold.

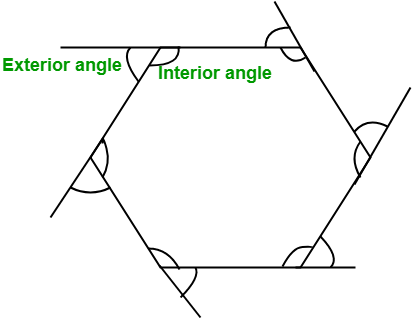
GMAT Polygon Properties

The polygon is basically a shape with more than 4 sides. It’s called regular when all the sides and internal angles are equal. In a regular polygon, all the triangles within are equilateral in nature. The exam requires an understanding of the properties of a regular polygon because an irregular polygon would have no consistent formula or properties.

• For a polygon, the number of sides can be used to determine the exterior angle property. 360/(Number of sides) = Exterior Angle Value, thus we can use the formula interchangeably to determine sides or exterior angle.
• A polygon is regular if all the internal angles/exterior angles are the same. We can draw the same conclusion.
• The sum of internal angles of a polygon (regular) is equal to (n-2)*180 degrees where n is the number of sides to the polygon.
• The sum of external angles is equal to 360 degrees. For a regular polygon, each external angle will be 360 degrees/n!

All Topics Indexed